State Logic

page 1
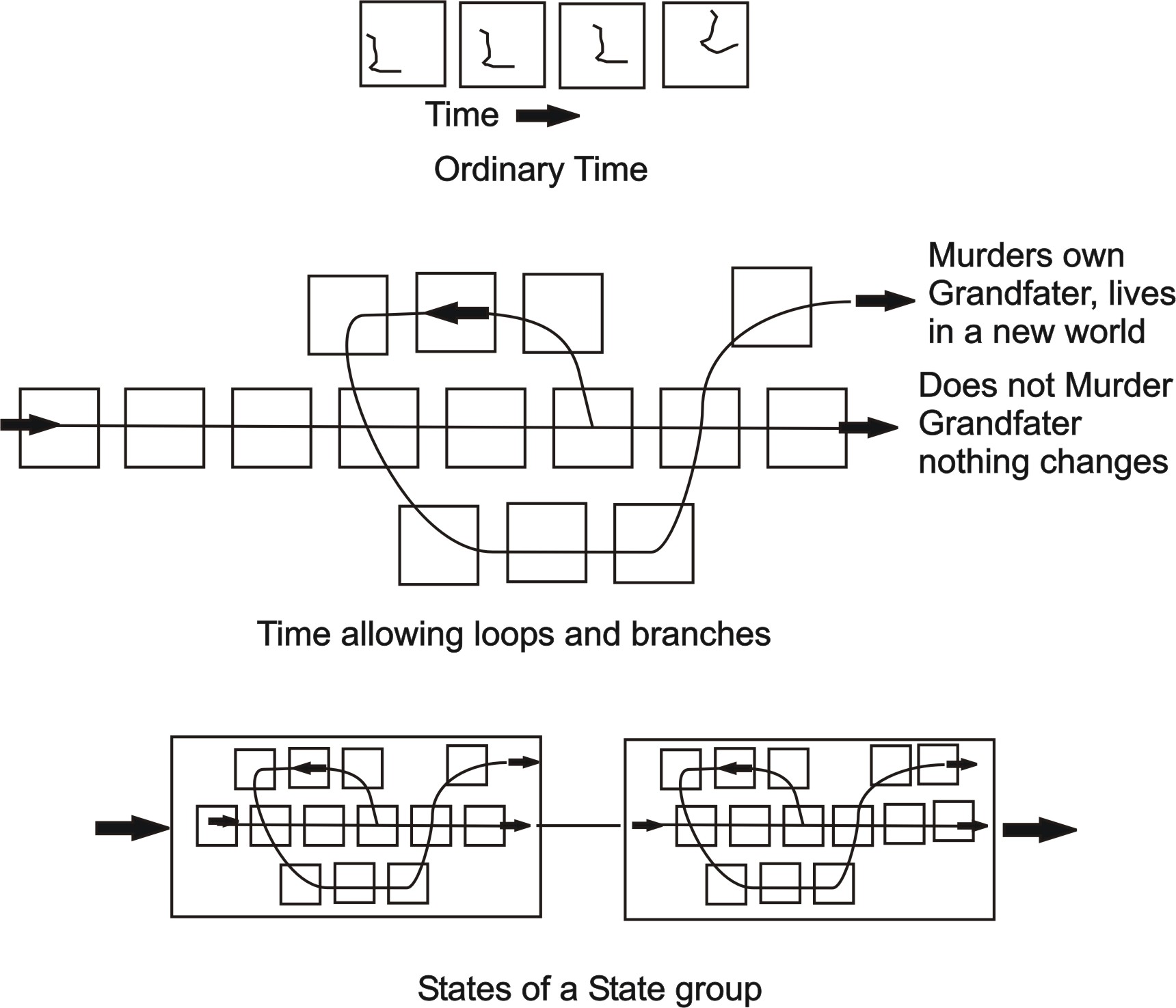
Paul Davies wrote in 9-02 Scientific American that time could be viewed as a series of states like the frames of a film. I think this idea has been around since Greek times but his article was very illustrative of current ideas about time.
If time is like this sequence of frames in a film you could play it in either direction and in fact physics of the small can not show any direction of time. Of course some might not agree and might believe that wave collapse is irreversible as well as uncertainty since you might get a different result every time you play the uncertainly film experiment, assuming that the film is an exact reproduction of reality.

In the frame system time is seen as a frozen series of states with no arrow of time inherent in the states. We know that time paradoxes cana be resolved by the many-worlds idea of quantum mechanics first proposed by Hugh Everett. The many-worlds interpreted as time states fits the film idea easily. All time paradoxes then become easy to resolve and are no longer paradoxes. Here below is one way to see how this works.

Of course the real situation would be much more complicated than this. Where the films intersect time travel has occured from one world to another world. Where the film branches either time travel is beginning or a quantum decision is invoked causing one world to branch off from another world. This example would be interpreted more as time travel than as quantum branching. We see that no pardoxes occur when states can intersect. Where they intersect you would have the time traveler meeting himself or herself but then any event change would cause branching avoiding any paradox. This is a very simplistic approach to some subtle ideas but it gets the basic idea accross that you can see everything as a series of states. Each frame represents a universe at an instant of time or in a specific state.

Above we illustrate one way that the state idea can be expanded by viewing a finite time sequences as another more complex set of frames. Many other state structures can exist only limited by our imaginations. The idea is very plastic and seems to be even more versatile than the main mathematical idea of sets and set theory but this is only a speculation at present. We will list a few of the possibilities.

page 2
1. The State of All States
This is similar to the concept of the set of all sets except that it forms an infinite number of sets of all sets as the film always advances to the next state of all states frame shot. If you try to freeze this and put it all into a single frame then that over all frame can advance to the next big overall frame to form sets of all sets of all sets and so on in infinite progress. In this sense the state of all states seems to be simpler than the set of all sets concept since it makes no attempt to form a final state of everything. It is just states as needed for the discussion or investigation at hand.

2. The State of Repeating the Same State
If a state contemplates itself would an infinity of states result as in the paradox of self reference? Any computer programmer knows the defeat of a program paradox such as an infinite loop. The computer freezes up and does nothing until it is unplugged and rebooted. Of course modern processors have a means of warning that an application is not responding and allows the user to end the program. An insane assylum probably has some patients who have too many infinite mental loops in their heads leaving not enough normal brain matter left over to have normal control of their mental states.

3. The State Where the Future is Forbidden
This is probably a state that will never be seen since it cannot advance into the future. Perhaps it only exists once as a frame shot and therefore you cannot prove it ever existed in the first place. Would a single vision of a ghost qualify?

4. The P State
P State is so named because when translated to set theory it is a paradox set. The idea is that state logic can include paradoxical stuff that loses the paradox feel when contemplated as a state system. For instance in electrical circuit logic a relay race is an infinite loop where a set of relays continuously turn on an off in a sequence similar to a simple pair of paradox statements. Here is an example "The next sentence is false. The previous sentence is true" Obviously wired electrically or in a program this would give an infinite loop of activity that requires at lest two repeating time states to operate continuously. In state logic it is just a two state system repeating forever. In that sense it is no longer a paradox. We have many mechanical systems that perform by cyclical repetition. Factories are modeled on this kind of system but they always build in stop switches. If there is no stop switch or means of stopping then we have a more natural system like an orbiting planet. In set theory this time element is usually missing but in state systems it is the main subject. Thus adding the P set to set theory simply emulates state theory. It would require a time variable to be added to mathematical theorems about P sets. In that case state theory might be seen as one step above set theory and set theory.

A Turing machine uses a state table and an infinite tape with square frames. Each frame contains blank or a symbol and the state table instructs the machine what to do based on what symbol it reads. It can erase and write a new symbol or just erase then move right or left. This a crude definition but the simplicity of the idea makes it possible to characterize the essence of a computer. We would like to compare this to natural state frames. In nature the state table is now the laws of physics and the frames of the tape are the states of the universe. Of course such a simple definition immediately seems inadequate to define nature or reality. What about quantum properties which are not explianed in a completely local manner? Would any kind of state machine be adequate to explain all the mysteries of quantum theory? Even so it is fun to speculate about state logic since it is so simple to understand the basic idea and seems to fit well with how our minds organize and store information.

page 3
The human brain is a very complex state machine, if it can be called that. When we remember things we can remember in many different ways either as a verbal recollection of what happened or as a visual sequence with just a few still frames of the experience. When we try harder or take time to recollect the mind can often reproduce the memory as if it were being relived in reality. In fact a few people have been identified with almost perfect autobiographical memory, covering every awake moment back to about 8 or 10 years old. It is as though the brain's memory capacity is many terabytes or many times larger than a one terabyte computer hard drive. The brain may not need such a large capacity by having compression techniques that far surpass anything presently known. Very little is known at present about how so much detail can be accessed by a single mind. Yet when tested these special people can recite exact dates, names, time of day and even what was said for important events they lived through, as well as trivial events such as riding in a car and seeing the number on a licence plate on the car ahead the cars color, the weather at the time the conversation if any or what was being said on the radio. Such an incredible amount of detail stored over many years is hard to comprehend. However with the present advance of technology this will soon become an ordinary feat for electronic devices.

The idea that our brain stores all this stuff in a sort of state stream that can be accessed at will is not difficult to imagine since we are all familiar with film and with pages of a book, writing in notebooks and so forth. So to refer to state logic to try to emulate nature is not a big stretch and fits naturally with the way we organize and form memories and think about things. It is much easier to separate things into distinct pictures where each picture shows a kind world of the instant it records even though it is restricted in both time and space. Without such a simplifying system it would be harder to cubbyhole things and make them availble for future access.

The brain is marvelous in being able to replay reality when desired or when daydreaming, almost as if it contains within it a multiverse of state films available for dreaming or imagining at will.

We want to emphasize that we think that state logic should contain a natural P state system which is the paradox states when time is removed. The simplest P state being states that turn on and off, on and off continuously, like a miswired or 'pardoxica'l relay race, or like truth telling false to turn on and false telling truth to turn off. These on off systems or repetitive systems being the main way that factories or any repetitive cyclical system operates. Nature by being mostly composed of cyclical actiions is then produced mainly by the actions of the Paradox state system.

The P state is a generalized idea that what is paradoxical when time is not included may not always be so paradoxical when time is included. Here is an example where perhaps time can include a paradox but can still accomodate it as a recurrance of the same circuit as already mentioned.

The following statement is false
The previous and following statements are true
The previous statement is false
repeat

It represents a continuous stream of repeating states where things turn on and off as the film plays forward in time. Does it play exactly the same when played backwards?

Note that in quantlum theory playing a film backwards is no longer adequate. This is because you need to reverse not just time but parity and charge conjugation due to an assymetry of the weak force interactions. To apply this to film you would need mirror image words and perhaps some reversed forces so the film would no longer look like time can be sensibly reversed in the traditional sense.

page 4
To conclude then we want to emphasize that we think that state logic should contain a natural P state system which is the paradox states. The simplest P state being states that turn on and off, on and off continuously, like a pardoxical relay race, or like truth telling false to turn on and false telling truth to turn off. These on off systems or repetitive systems being the main way that factories or any repetitive cyclical system operates. Nature by being mostly composed of cyclical actiions is then produced mainly by the actions of the Paradox state system.

Finally we want to make a bunch odd statements about states to get the effect of state system thinking that the brain seems to have a natural feel for. This is a speculative and somewhat recreational or entertaining conclusion to this old idea. You can view the singular word state as sometimes meaning a series of states or an infinite series of states.

1. The state of entertainment. 2. A state of illness. 3. A state ment about states. 4. A state of mind. 5. Alice in state land. 6. The state where futures are forbidden. 7. The state where states all play backwards except the present state. 8. The state where forces are reversed except gravity. 9. The state of happyness 10. A state of infinite lists. 11. The null states or the set of all states where nothing exists. 12. The states where Godel's theorems can't exist. 13. States of no motion. 14. The state where gravity repels. The many states of mathematics.

As you can see the word and the concept can mix together in confusing ways yet individual statements seem to cohere as being about states or a state. State logic as we use it is just a convenient way of compartmentalizing the passage of time.

page 5

Mathematics as States
page 6

Why is a time variable seldom seen in a mathematical equation? This is because time is assumed as automatic and unnecessary. We postulate some items to show this.

1. The number 1 written on a piece of paper continuously cycles thru time. If you see it again tomorrow it has cycled thru one day of time. The paper exists in a time line therefore the symbol on it exists in repeating units of time. The same is true of any equation.

2. The mind also cycles the number 1 in a re-circulating mental circuit when it contemplates or uses it. In this way time is automatic in mathematics. A time variable only comes into play explicitly when needed such as a velocity.

3. To become more aware of how time is ingrained in mathematics we propose a way of looking at an equation or a number as a system of states. The number 1 would be a repeating set of film frames showing the number 1. You then see it as existing only by the action of time.

Every mathematical manipulation has a state number S = s+1 = number of steps plus 1.
The list of manipulations is the state list which is the frames of the film or the list of states.

Sometimes given just parts of a state list it is possible to reconstruct the whole list, or play a state game. We can then list some of the things used in a mathematical manipulation, at least involving solving an equation. For an equation such as y=4+5*3-6*2 we have a state number, Sn = 5. To this we can add a State list of operators Sop = +,*,-,*. In addition we have the elements Se = y,4,5,3,6,2. In a crude but interesting analogy with physics Sn is like sn energy level, Sop are like forces, and Se are like particles. The equal sign may or may not be included as an op. Continuing the analogy we can see mathematicians brains as colliders of equation particles.

We can create a game of mathematical bread crumbs by only listing parts of the Sn, Sop, Se at each state. Object: find the original expression. For instance given a list 4,8,17 what simplest expression produced it? One answer might 4*2+9. Another answer is 4+4+9. The second answer might be preferable as being simpler. You could also be given 4,,17,*. Thus 4*2+9 or 4*3+5 would work. Given 4,2,*,+ we could have 4-3*16+1. This is not preferred since it includes a negative sign and we want to get as close to the given state list as possible so 4*2+7 seems to be best as it includes only 1 extra list number n=7.

We see that to arrive at a # such as 6 and infinity of different ways is possible. This is not like a qubit where the qubit is both a 0 and a 1. It is never 1/2 or 1/3 or some real number in between. It is 0 and 1, only two possibilities while math can get to 6 in an infinity of ways. There is a similarity with entanglement in that we would like to limit our bread crumb game to very few and very simple elements. For instance one expression for 6 is 6=1/6*6*6*1/30*30. We have Sn=5, and Sl=1/6,6,6,1/30,30, if we treat simple fractions as single numbers, and 4 Sop=*,*,*,*. The main idea of such a game is to develop a feeling for the time aspect of mathematics. It can only exist as moving circuitry, it is never just ink on paper which alone contains zero meaning and has zero effect on anything. The game could continue to develop eventually incorporating more and more of mathematics, geometry and topology.

All this state logic brings up the subject of times arrow or the non-reversible nature of time in mathematics. For instance once you have a result if you do not know how the result was gotten you probably and usually cannot reproduce exactly the manipulations that produced the result. The result is like a wave collapse and uncertainty in quantum mechanics as a very crude but illustrative analogy. You do not get to fully reverse things that have slipped away. Mathematicians and logicians would object strenuously saying that different ways of obtaining the same result are equivalent. And I do not object, I only want to point out how much we take for granted when we make our powerful generalizations. In fact by investigating these processes in detail we might reveal new knowledge about logic an math not previously obvious.

page 7

We can point out other simple uncertainties in any result. For instance given Sr=1(Sr is the result) and Sop=*, two equally simple answers are possible -1*-1=1 and 1*1=1. If square root is the op and 1 the list then you could also have the same two possible manipulations in reverse as equally valid answers showing that uncertainty is built into mathematical information. Another very deep uncertainty is the inability to get absolute exactness when using real numbers applied to the real world. Nature seems to exploit this powerful continuity or quantum non ability to not always round off to the nearest quantum metric in producing her chaos, which is at work pretty much everywhere we look and even in our own thoughts and heartbeats.

Temporal or non time reversible operations are defined by quaternions and Octonions. For instance ij=k and ji=-k. Since we always tend to work equations and operations in a left to right manner we see time moving left to right predominantly as we think mathematically. To alert our minds to this when using ijk operators we propose to invent a substitute for equals such as >>> and <<<. Then ij>>>k and ji>>>-k. Reversing time we can go right to left and write

k<<<ji and -k<<<ij.

These anti expressions then annihilate as

( ij>>>k)+(-k<<<ij)=0

The new signs for equals could always be used in place of = to remind us that time is an important element in our every detail of thinking and might give humans an edge in expanding our understanding of the great power of mathematics. Writing a simple expression like 1>>>1 or if a>>>b and b>>>c the a>>>c and reversing c<<<a because c<<<b and b<<<a. You can see how difficult it is to reverse our time line of thinking for fairly simple ideas without going all the way and writing in mirror image and reading from right to left and Leonardo seemed to be fond of doing.