PUZZLEATOMICtM
In how many ways can you link 4 circles, 5 circles, or n circles so that every pair is linked called all linked circles? The paper "Integer Code for Linked Circles" (Rev. 1-2018) reveals a simple integer code for the simplest kinds of all linked circles. Mathematical twist invariants are produced using a list of Integers. The integer code can be used to generate mirror image links by writing the integer list in reverse. The code can calculate the linking number/twist and other interesting properties. Linked circles develop a natural hierarchy of self organizing complexity as n increases.
Research ongoing... New link to Quantum Circle knots

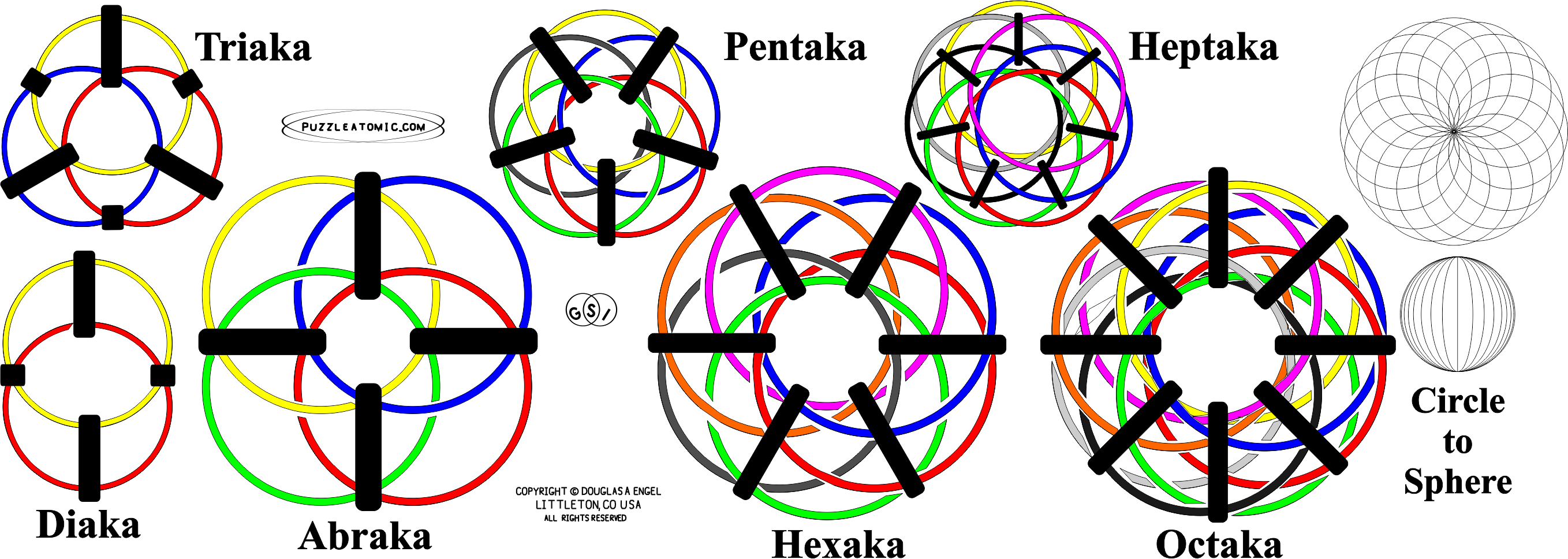
The solid circular links held by "node keepers," as shown here can appear to turn inside out, from a flat shape to a spherical shape, with holes at the poles, then back to a flat shape. If the circles are thin enough then you can make a large n-aka like this. The circles can be linked in any manner as long as every circle links exacly once thru all the other circles. This is similat to a Hopf fibration except for the addition of node keepers to maintian flat symmetry. The n-aka matrix twists could be calculated with the twist calculator below. The right most figure shows how an "infinite circle aka" could turn from a flat circle with diameter 2D into a sphere with diameter D, with some way to preserve the node symmetry. n-Aka system copyright 2015, Douglas A. Engel, Littleton, CO.
Integer Code for Linked Circles(paper Integer Code for Linked Circles) Revised Jan./6/2017. New Rogue links added. Revised Jan/Feb/2018. New linkage composition and image, mirror image composition added Have you ever wondered in how many ways you can link n identical circles together? It is simple if n is about 5 or less. It becomes harder with n greater than 5 and is even tricky for n=5. When n is 7 you can make a Rogue link, a very rascally thing. This pdf paper develops the mathematical twist of a certain set of linked circles. Only elementary arithmetic required to read and understand. New additions to this paper include a Matrix total twist invariance property. You can view this property when you experiment with the twist calculator below. Starting with a single circle then a link of two circles and progressing to links of several circles, a method of specifying a linear link with a sequence of integers is given and the calculator below is produced. Five circles can be linked so that no circle can be paired with any other circle without removing a circle and is called the first Aclk1 prime. How many twists can each circle of a link of 10,000 circles have? ( disabled prev 2017 revs., Maximally linked Circles With Invariants)(disabled prev revs. 4/2016, 10/2016 Marked Circle Links With Invariants)
ALL LINK SYSTEMS INITIAL RESEARCH (a pdf research paper showing photos of several of the linkages, methods of derivation and number results)
ACL TWIST CALCULATOR is a circle drawing and linkage twist calculator for up to 20 linked circles . This was written by Troy Black using my calculation method. The ACL calulator now gives the CC matrix and the FO matrix. You can use the drop down on either matrix and click to use that for a new matrix calculation The circle display shows how the circles are actually linked. ACL TWIST CALC 30 circles.
To use this calculator enter each positive integer 1 thru n, in any order(maximum of 20) separated by commas and click the Calculate button. There must be at least 2 numbers, such as 1,2 or 2,1 which is the simplest linkage of 2 circles. 1,2 gives a twist of 1 while 2,1 gives a twist of -1. If you enter the integers in a counting sequence such as 1,2,3,4... this will produce a maximal twist. In reverse order it produces a maximun negative twist. A sequence such as 1,2,3,6,5,4 will produce zero twist with three circles twisted one way and three circles twisted the other way.